2023年
第1問
(1) $x$方向は速度一定ゆえ,
$$t_1 = \textcolor{#ff981f}{ \frac{\ell_1}{v_0 \cos \theta} }~.$$
(2) 運動方程式($y$方向)より,
$$a_1=\textcolor{#ff981f}{ -\frac{eE_1}{m} }~.$$
(3) $t=t_1$に$y=0$となるために,
$$\begin{split} &v_0 \sin \theta \cdot t_1+\frac{1}{2} a_1 t_1{}^2=0\\ &\therefore~E_1=\textcolor{#ff981f}{ \frac{2 m v_0{}^2 \sin \theta \cos \theta}{e \ell_1} }~. \end{split}$$
(4) 円軌道の半径を$r_2$して, 運動方程式(中心方向)より,
$$\begin{split} &m\frac{v_0{}^2}{r_3}=e v_0 B_2\\ &\therefore~r_3=\frac{mv_0}{eB_2}~. \end{split}$$
すると, 中心の$y$座標は,
$$y_2=-h+r_3=\textcolor{#ff981f}{ -h+\frac{m v_0}{e B_2} }~.$$
(5) $\ell_2=r \sin \theta$と表されることから,
$$B_2=\textcolor{#ff981f}{ \frac{m v_0\sin \theta}{e\ell_2} }~.$$
(6) 運動の磁場に垂直な面上への射影は等速円運動であり,その半径は$r_3=\dfrac{m v_0 \sin \theta}{e B_3}$である.その周期は,
$$T_3=\frac{2 \pi r_3}{v_0 \sin \theta}=\textcolor{#ff981f}{ \frac{2 \pi m}{e B_3} }~.$$
(7) $x$方向の運動は,加速度 $a_3=\dfrac{e E_3}{m}$の等加速度運動である.時刻$t=NT_3$に原点に戻ることから,
$$\begin{split} &-v_0\cos\theta\cdot NT_3+\frac{1}{2}a_3(NT_3)^2=0\\ &\therefore~E_3=\textcolor{#ff981f}{ \frac{v_0 B_3 \cos \theta}{\pi N} }~. \end{split}$$
(8) $\displaystyle -v_0\cos\theta +a_3\cdot\frac{NT_3}{2}=0$より,
$$\ell_3 = \textcolor{#ff981f}{ \frac{1}{4} N v_0 T \cos \theta }~.$$
(9) 電子は原点に戻って以降は,図1と同じ運動をする.速さ$v_0$でDへ入射した電子が,電圧$V$で減速されてもなおYに到達するためには,$\dfrac{1}{2}mv_0{ }^2-eV\geqq 0$$より,
$$v_0 \geqq \textcolor{#ff981f}{ \sqrt{\frac{2eV}{m}} }~.$$
(10) 電流の大きさは$I=en$ゆえ,
$$V=R I=\textcolor{#ff981f}{ Ren }~.$$
(11) コンデンサー(容量$C=\varepsilon_0 \dfrac{S}{d}$)の電圧も$V$であるから,電荷は,
$$Q=C V=\textcolor{#ff981f}{ \frac{\varepsilon_0SRen}{d} }~.$$
(12) コンデンサーの電荷の変化量は,$\varDelta Q = en\varDelta t$ゆえ,静電エネル ギーの変化量は,
$$\begin{split} \varDelta U & =\frac{(Q+\varDelta Q)^2}{2 C}-\frac{Q^2}{2C}\\ &=\textcolor{#ff981f}{ \left(R+\frac{d}{2\varepsilon_0 S}\varDelta t\right)(en)^2\varDelta t }~. \end{split}$$
第2問
(1) 過程2→3で気体がした仕事は,
$$W_{23}=\textcolor{#ff981f}{ p_2(V_3-V_2) }~.$$
(2) 過程2→3で気体での気体の内部エネルギー変化は,
$$\varDelta U_{23} = \textcolor{#ff981f}{ nC_V(T_3-T_2)}~.$$
(3) 過程4→1での気体の放熱量は,気体の内部エネルギーの減少量に等しく,
$$Q_{41}^* = \textcolor{#ff981f}{ nC_V(T_4-T_1) }~.$$
(4) 断熱過程では,気体がした仕事は内部エネルギーの減少分に等しい.過程1→2,3→4で気体がした仕事は,
$$\begin{split} &W_{12} = -nC_V (T_2-T_1)~(<0)~,\\ &W_{34} = -nC_V (T_4-T_3)~(>0)~. \end{split}$$
また,気体定数は$R=C_p-C_V$と表されるので,
$$W_{23}=n(C_p-C_V)(T_3-T_2)~.$$
よって,1サイクルの間に, 気体がした正味の仕事は,
$$\begin{split} W_\text{cycle}&=W_{12}+W_{23}+W_{34}\\ &=\textcolor{#ff981f}{ nC_p(T_3-T_2)-nC_V(T_4-T_1) }~. \end{split}$$
※ 過程2→3での吸熱量$Q_{23}=n C_p(T_3-T_2)$を用いて,$W_\text{cycle}=Q_{23}-Q^*_{41}$と考えてもよい.
(5) 熱効率は$e=\dfrac{W_\text{cycle}}{Q_{23}}$であるから,$f=1-e$は,
$$f = \textcolor{#ff981f}{ \frac{T_4-T_1}{\gamma (T_3-T_2)} }~.$$
(6)
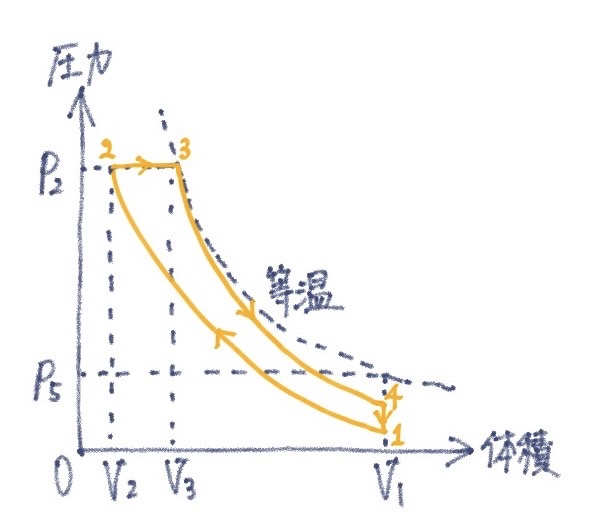
※ 等温線より断熱線の方が急勾配であることに留意する.
(7) $T_2\left(\dfrac{V_1}{a}\right)^{\gamma-1}=T_1 V_1{}^{\gamma-1}$より,
$$T_2 =\textcolor{#ff981f}{ a^{\gamma -1}T_1 }~.$$
(8) $T_3=\frac{V_3}{V_2} T_2$より,
$$T_3 =\textcolor{#ff981f}{ a^{\gamma -1}bT_1 }~.$$
(9) $T_4 V_1^{\gamma-1}=T_3\left(\dfrac{bV_1}{a}\right)^{\gamma-1}$より,
$$T_4=\textcolor{#ff981f}{ b^\gamma T_1 }~.$$
(10)
$$f=\textcolor{#ff981f}{ \frac{b^\gamma-1}{\gamma a^{\gamma-1}(b-1)} }~.$$
(11) モル数が増えてもポアソンの公式の立式は変わらない.また,同体積・同温度では,圧力はモル数に比例する.よって,
$$\frac{T_2^{\prime}}{T_2}=\textcolor{#ff981f}{ 1 }~,\quad\frac{p_2{ }^{\prime}}{p_2}=\textcolor{#ff981f}{ 1.4 }~.$$
(12) 吸熱量や仕事はモル数に比例する.よって, 仕事の総和は$\textcolor{#ff981f}{1.4}$倍で,熱効率は$\textcolor{#ff981f}{1}$倍となる.