2023年度前期
第1問
問1 台の運動方程式より,
$$ \begin{split} &M(-a)=-F+\mu^{\prime}mg\\ &\therefore~F = \textcolor{#ff981f}{ Ma+\mu^{\prime}mg }~. \end{split} $$
なお,小物体の加速度(右向き正)を$b$とすれば,小物体の運動方程式より,
$$m b=-\mu^{\prime} mg~.$$
問2 台が止まる時刻は$t_1=\dfrac{v_0}{a}$である.この間の相対変位の大きさは,
$$\frac{1}{2}(v_0+bt_1)t_1 = \textcolor{#ff981f}{ \frac{1}{2}(a-\mu^{\prime}g)\left(\frac{v_0}{a}\right)^2 }~.$$
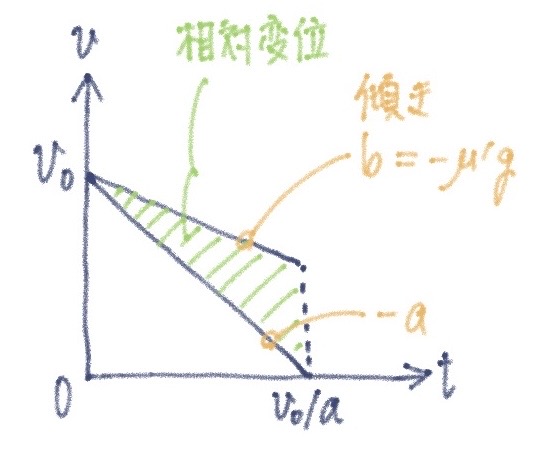
問3 台の加速度は$B=\dfrac{\mu^{\prime}mg}{M}$となり,小物体の加速度は$b$のままである.台と小物体の速度が一致する時刻を$t_1+T$として,
$$ \begin{split} &\left(v_0+bt_1\right)+bT=BT\\ &\therefore~ T=\textcolor{#ff981f}{ \frac{M\left(a-\mu^{\prime} g\right) v_0}{\mu^{\prime}(M+m)ga} } \end{split} $$
問4
$$BT=\textcolor{#ff981f}{ \frac{m}{M+m}\left(1-\frac{\mu^{\prime} g}{a}\right) v_0 }~.$$
問5
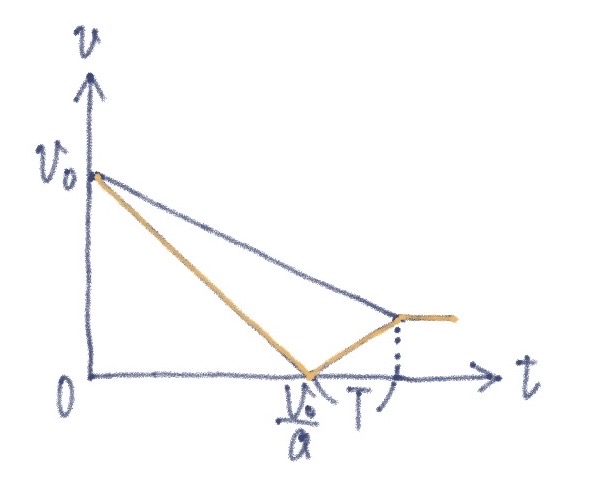
第2問
問1 AP間,BP間とも抵抗値は$R$である.S-on直後,コンデンサの電位差はゼロゆえ,全体の合成抵抗は,
$$\left(\frac{1}{R}+\frac{1}{R}\right)^{-1}+\left(\frac{1}{R}+\frac{1}{2 R}\right)^{-1}=\frac{7}{6} R~.$$
よって,求める電流は,$I=\textcolor{#ff981f}{\dfrac{6 V}{7 R}}$となる.
問2 充分経過後,コンデンサへの電流は止む.このときの全体の合成抵抗は,
$$\left(\frac{1}{2 R}+\frac{1}{3 R}\right)^{-1}=\frac{6}{5} R~.$$
よって,求める電流は,$I= \textcolor{#ff981f}{ \dfrac{5V}{6R} }$となる.また,このとき,コンデンサの電圧は$\dfrac{2}{3}V-\dfrac{1}{2}V=\dfrac{1}{6}V$ゆえ,電荷は,$Q= \textcolor{#ff981f}{ \dfrac{1}{6}CV }$である.
問3 時間が経過しても電流が変化しなかったということは,終始コンデンサへ電流が流れなかったということ.よって,$x: 1-x=R: 2 R$より,$x= \textcolor{#ff981f}{ \dfrac{1}{3} }$となる.
※ ここまで’21共テ物理(第1日程)第2問と同趣旨の問題.
問4 このときの全体の合成抵抗は,
$$ \begin{split} R_\mathrm{T} &=\left(\frac{1}{x \cdot 2 R}+\frac{1}{R}\right)^{-1}+\left\{\frac{1}{(1-x) \cdot 2 R}+\frac{1}{R}\right\}^{-1}\\ &= \textcolor{#ff981f}{ \left(\frac{x}{2 x+1}+\frac{1-x}{3-2 x}\right) \cdot 2R }~. \end{split} $$
問5 全体での消費電力は$P=\dfrac{V^2}{R_\mathrm{T}}$で与えられるから,$R_\mathrm{T}$が最大のときに$P$は最小となり,$R_\mathrm{T}$が最小のときに$P$は最大となる.
$$ R_\mathrm{T} = \frac{4 x^2-4 x-1}{4 x^2-4 x-3} \cdot 2 R = \left(1+\frac{2}{4 x^2-4 x-3}\right) \cdot 2 R~. $$
よって,$x=\dfrac{1}{2}$のときに$P_{\text {max }}=\textcolor{#ff981f}{ \dfrac{V^2}{R} }$となり,$x=0,~1$のときに$P_{\text {min }}= \textcolor{#ff981f}{ \dfrac{3 V^2}{2 R} }$となる.
第3問
問1
ア $0\leqq\beta < \alpha$の場合,光路差の大きさは,
$$\varDelta s= \textcolor{#ff981f}{ L \{\sin \alpha+\sin (\alpha-\beta)\} }~.$$
イ $\beta\geqq\alpha$の場合には,
$$\varDelta s= \textcolor{#ff981f}{ L |\sin \alpha+\sin (\beta -\alpha)| }~.$$
この表式はアの場合も含んでいる.
ウ 入射角と反射角が等しくなるとき,$\beta=\textcolor{#ff981f}{ 2(\alpha-\theta) }$が成り立つ.
エ この場合も,$\beta=\textcolor{#ff981f}{ 2(\alpha-\theta) }$である.
オ $\beta=0$のとき,$\alpha=\textcolor{#ff981f}{ \theta }$である.
カ $\beta=0$,$\alpha={ \theta }$のとき,強めあう条件$\varDelta s = m\lambda$は,
$$2 L \sin \theta=m \lambda$$
となる.これを満たす$\lambda$のうち最も大きいものは,$m=1$に対応するので,
$$L= \textcolor{#ff981f}{ \frac{\lambda_\mathrm{L}}{2 \sin \theta} }~.$$
キ $\beta={ 2(\alpha-\theta) }$の下で,経路差の大きさは,
$$\varDelta s = \frac{\lambda_\mathrm{L}}{2 \sin \theta}|\sin \alpha-\sin (\alpha-2 \theta)|$$
を和積公式で整理して,
$$\varDelta s = \textcolor{#ff981f}{ \lambda_\text{L}\cos (\alpha-\theta) }~.$$
ク $\varDelta s= \textcolor{#ff981f}{ \lambda_\text{L}\cos (\alpha-\theta) }~.$
※ 絶対値は不要.
※ 大学公表の正解は,和積公式で整理する前段階の式となっていた.
問2 $\alpha=70^{\circ}$,$\theta=10^{\circ}$のとき, 反射光が強めあう条件は,
$$\lambda_L \cos 60^{\circ}=m \lambda~.$$
ここに$\lambda=190\,\text{nm}$を代入すれば,$\lambda_\text{L}=m \times 380\,\mathrm{nm}$となる.$m=1$に対応するものは表にないが,$m=2$に対応するものはあり,それが$\textcolor{#ff981f}{\text{I}}$である.
第4問
問1 状態方程式より,温度はA,Bとも$T_0=\textcolor{#ff981f}{\dfrac{p_0 S L}{R}}$である.
問2 ピストンのつりあいより,
$$p_\text{B}= \textcolor{#ff981f}{ p_\text{A}+\frac{mg}{S} }~.$$
問3 AとBの温度が等しいことから,
$$p_\text{A} \cdot S(L+x)=p_\text{B} \cdot S(L-x)~.$$
よって,
$$p_\text{A}=\textcolor{#ff981f}{ \frac{m g}{2 S}\left(\frac{L}{x}-1\right)~. }$$
問4 Aの内部エネルギー変化は,
$$ \begin{split} \Delta U_\text{A} = &\frac{5}{2}p_\text{A} \cdot S(L+x)-\frac{5}{2}p_0\\ = &\textcolor{#ff981f}{ \frac{5}{2}\left\{\frac{mg\left(L^2-x^2\right)}{2 x}-p_0 S L\right\} }~. \end{split} $$
なお,AとBはモル数も温度変化も等しいため,内部エネルギー変化も等しい.よって,系全体のエネルギー保存則より,
$$2\Delta U_\text{A}+mg(-x)=0$$
となり,これより$m$と$x$の対応関係が得られる:
$$m = \frac{10Lx}{5L^2-7x^2}\frac{P_0 S}{g}~.$$
問5 $x=\dfrac{4}{5}L$として,
$$m^\prime=\textcolor{#ff981f}{ \frac{200}{13} \frac{P_0 S}{g} }~.$$